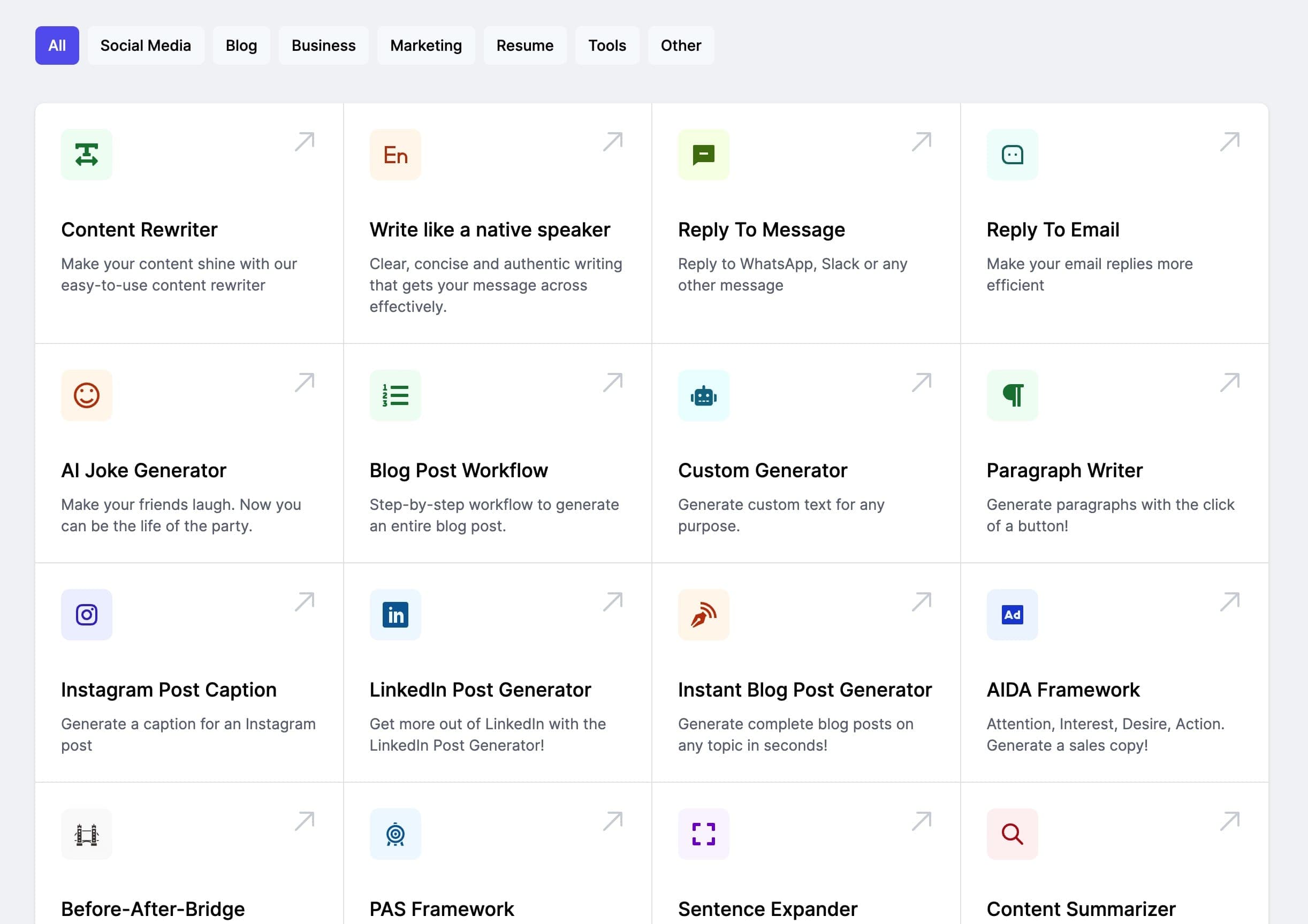
19+20=1 36+25=0 ここで問題です(↑ヒント) 905+80=?
[Analysis]
提示された問題は、数値データを用いたパターン認識の問題です。統計的な視点(回帰分析や関数推定)で捉えると、入力変数(左辺の数値)と出力変数(右辺の数値)の間に存在する隠れた法則 $f(x, y)$ を見つけ出すタスクとなります。通常の算術演算(加算)では成立しない等式(19+20=1 など)が含まれているため、数値の量的価値ではなく、その「形状」や「特性」に基づいた変数変換が必要であると推測されます。ここでは、各数字が持つ「閉じた領域(穴)」の数に着目し、そのカウントデータを用いたモデル化を行います。
[Solution]
ステップ1:変数の定義とデータ変換
数字の形状に基づき、各数字が持つ「穴」の数をカウントするマッピングルールを定義します。
穴が1つの数字:0,4,6,9 $\to$ 値は 1
穴が2つの数字:8 $\to$ 値は 2
穴がない数字:1,2,3,5,7 $\to$ 値は 0
ステップ2:学習データ(ヒント)の分析
提示された等式を用いて、演算ルール(モデル)を推定します。
ケース1:19+20=1
左項 19 の特性値:
1(穴0)+ 9(穴1)= 1右項 20 の特性値:
2(穴0)+ 0(穴1)= 1結果との関係:
変換された値 1 と 1 から結果 1 を得る演算は、乗算 1×1=1 が適合します。
ケース2:36+25=0
左項 36 の特性値:
3(穴0)+ 6(穴1)= 1右項 25 の特性値:
2(穴0)+ 5(穴0)= 0結果との関係:
変換された値 1 と 0 から結果 0 を得る演算は、ここでも乗算 1×0=0 が適合します。
ステップ3:モデルの確定
以上の分析から、このシステムの法則は以下の通りであると断定できます。
「(左の数値の穴の総数)$\times$(右の数値の穴の総数)= 答え」
ステップ4:ターゲットデータの計算
確定したモデルを問題の式 905+80 に適用します。
左項 905 の特性値計算:
9 $\to$ 1
0 $\to$ 1
5 $\to$ 0
合計:1+1+0=2
右項 80 の特性値計算:
8 $\to$ 2
0 $\to$ 1
合計:2+1=3
最終演算:
法則に従い、算出した特性値を掛け合わせます。
2×3=6
[Answer]
6